On Recursion 1 - Alex Jiang

These series are the reflection and study when I was leading an engineering team for all the aspects of software development. In this post, we will explore an important technique, recursion 🌿, which, it’s a concept that many people scratch their heads over.

A recursive function is defined in terms of base cases and recursive steps:

In a base case, we compute the result immediately given the inputs to the function call
In a recursive step, we compute the result with the help of one or more recursive calls to this same function, but with the inputs somehow reduced in size or complexity, closer to a base case.

Consider writing a function to compute factorial:

The factorial

demo

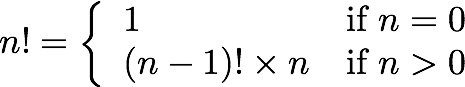
And we have the recursive implementation in Swift:

public static func factorial(n: Int) -> Int {
  if n == 0 {
    return 1
  } else {
    return n * factorial(n-1)
  }
}

For the above implementation, the recursive step is n > 0 , where we compute the result with the help of a recursive call to obtain (n-1)!

To visualize the execution of a recursive function, let’s diagram🎨 the call stack of currently-executing functions as the computation proceeds.

Suppose we run the factorial function inside main thread as follows:

let x: Int = factorial(3)

starts in `main`	calls `factorial(3)`	calls `factorial(2)`	calls `factorial(1)`	calls `factorial(0)`	returns to `factorial(1)`	returns to `factorial(2)`	returns to `factorial(3)`	returns to `main`
main	factorial n = 3 main x	factorial n = 2 factorial n = 3 main x	factorial n = 1 factorial n = 2 factorial n = 3 main x	factorial n = 0 returns 1 factorial n = 1 factorial n = 2 factorial n = 3 main x	factorial n = 1 returns 1 factorial n = 2 factorial n = 3 main x	factorial n = 2 returns 2 factorial n = 3 main x	factorial n = 3 returns 6 main x	main x = 6

In the diagram, we can see how the stack grows:

main calls factorial
factorial then calls itself , until factorial(0) does not make a recursive call
the call stack unwinds, each call to factorial returning its answer to the caller, until factorial(3) returns to main

Here’s an interactive visualization of factorial. You can step through the computation to see the recursion in action.

The factorial

TBD..